Fields Medal Winners

The Fields Medal is the premier award in Mathematics - often referred to as the "Nobel Prize for Mathematics". The prize was founded by John Charles Fields. In January 1932, Fields indicated that the idea of the medal had the support of the major mathematical societies of France, Germany, Italy, Switzerland and the United States, and he also outlined the principles behind the proposed medal. The genesis of the rule that it be awarded only to mathematicians no older than forty is evidently the statement that “… while it was in recognition of work already done, it was at the same time intended to be an encouragement for further achievement on the part of the recipients and a stimulus to renewed effort on the part of others”. The medal became known as the Fields Medal and was first presented at the International Congress in 1936. There was then a break for the war and the medals were next presented in 1950. Every four years since then up to four fields medals have been presented, and the next set of medals will be presented in 2006. Below I list the names of the recipients of the Fields Medal and the areas of Mathematics for which they received the award.

1936

Lars Valerian AHLFORS (Harvard University) - Awarded medal for research on covering surfaces related to Riemann surfaces of inverse functions of entire and meromorphic functions. Opened up a new ideas in analysis.

Jesse DOUGLAS (Massachusetts Institute of Technology) - Did important work of the Plateau problem which is concerned with finding minimal surfaces connecting and determined by some fixed boundary.

1950

Laurent SCHWARTZ (University of Nancy) - Developed the theory of distributions, a new notion of generalized function motivated by the Dirac delta-function of theoretical physics.

Atle SELBERG (Institute for Advanced Study) - Developed generalizations of the sieve methods of Viggo Brun; achieved major results on zeros of the Riemann zeta function; gave an elementary proof of the prime number theorem (with P. Erdös), with a generalization to prime numbers in an arbitrary arithmetic progression.

1954

Kunihiko KODAIRA (Princeton University) - Achieved major results in the theory of harmonic integrals and numerous applications to Kählerian and more specifically to algebraic varieties. He demonstrated, by sheaf cohomology, that such varieties are Hodge manifolds.

Jean-Pierre SERRE (Collège de France) - Achieved major results on the homotopy groups of spheres, especially in his use of the method of spectral sequences. Reformulated and extended some of the main results of complex variable theory in terms of sheaves.

1958

Klaus Friedrich ROTH (University of London) - Solved in 1955 the famous Thue-Siegel problem concerning the approximation to algebraic numbers by rational numbers and proved in 1952 that a sequence with no three numbers in arithmetic progression has zero density (a conjecture of Erdös and Turán of 1935).

René THOM (University of Strasbourg) - In 1954 invented and developed the theory of cobordism in algebraic topology. This classification of manifolds used homotopy theory in a fundamental way and became a prime example of a general cohomology theory.

1962

Lars HÖRMANDER (Stockholm University) - Worked in partial differential equations. Specifically, contributed to the general theory of linear differential operators. The questions go back to one of Hilbert's problems at the 1900 congress.

John Willard MILNOR (Princeton University) - Proved that a 7-dimensional sphere can have several differential structures; this led to the creation of the field of differential topology.

John Willard Milnor (b. February 20, 1931) is a mathematician known for his work in differential topology and K-theory and his influential books, which are widely considered to be examples of fine mathematical writing. He won the Fields Medal in 1962. As of 2005, John Milnor is a distinguished professor at Stony Brook University, with his wife Dusa McDuff.

As an undergraduate at Princeton University he was named a Putnam Fellow in 1949 and 1950 and also proved the Fary-Milnor theorem. He continued on to graduate school at Princeton and wrote his thesis, entitled isotopy of links, which concerned link groups (a generalization of the classical knot group) and their associated link structure. His advisor was Ralph Fox. Upon completing his doctorate he went on to work at Princeton.

In 1962 Milnor was awarded the Fields Medal for his work in differential topology. He later went on to win the National Medal of Science (1967), the Leroy P Steele Prize for Seminal Contribution to Research (1982), the Wolf Prize in Mathematics (1989), and the Leroy P Steele Prize for Mathematical Exposition (2004).

He has been editor of the Annals of Mathematics since 1962. His books include Topology from the Differentiable Viewpoint, Morse Theory, Characteristic Classes (with Stasheff), The h-Cobordism Theorem, Dynamics in One Complex Variable, and Singular Points of Complex Hypersurfaces.

His most celebrated single result is his proof of existence of 7-spheres with nonstandard differential structure. Later with Kervaire, he showed the 7-sphere has 15 differentiable structures (28 if you consider orientation). An n-sphere with nonstandard differential structure is called an exotic sphere.

His students have included Michael Spivak, John Mather, and Tadatoshi Akiba.

1966

Michael Francis ATIYAH (Oxford University) - Did joint work with Hirzebruch in K-theory; proved jointly with Singer the index theorem of elliptic operators on complex manifolds; worked in collaboration with Bott to prove a fixed point theorem related to the "Lefschetz formula".

Sir Michael Francis Atiyah, OM, FRS (born 22 April 1929) is a British mathematician. His path-breaking work with Isadore Singer led to the proof of the Atiyah-Singer index theorem in the 1960s, a result that has helped to pave the way for the development of several branches of mathematics since that time.

He had also founded, earlier and together with Friedrich Hirzebruch, the study of another major tool in algebraic topology: topological K-theory. It was inspired by Alexander Grothendieck's work on generalising the Riemann-Roch theorem, and has since generated algebraic K-theory and many applications to mathematical physics.

In 1966, when he was thirty seven years old, he was awarded the Fields Medal, for his work in developing K-theory, a generalized Lefschetz fixed-point theorem (jointly with Raoul Bott) and the Atiyah-Singer theorem, for which he also won, in 2004, the Abel Prize jointly with Isadore Singer.

Among the other prizes he has received are the Feltrinelli Prize from the Accademia Nazionale dei Lincei (1981) and the King Faisal International Prize for Science (1987).

Atiyah was knighted in 1983 and made a member of the Order of Merit in 1992.

Paul Joseph COHEN (Stanford University) - Used technique called "forcing" to prove the independence in set theory of the axiom of choice and of the generalized continuum hypothesis. The latter problem was the first of Hilbert's problems of the 1900 Congress.

Paul Joseph Cohen (born April 2,1934) is an American mathematician. He was born in Long Branch, New Jersey and graduated in 1950 from Stuyvesant High School in New York City.

He then studied at Brooklyn College for his bachelor's degree of 1953. At the University of Chicago, he received his master's degree in 1954 and his PhD in 1958.

He is noted for inventing a technique called forcing which he used to show that neither the continuum hypothesis nor the axiom of choice can be proved from the standard Zermelo-Fraenkel axioms of set theory. In conjunction with the earlier work of Gödel, this showed that both these statements are independent of the Zermelo-Fraenkel axioms: they can be neither proved nor disproved from these axioms. For his efforts he won the Fields Medal in 1966. He was also awarded the Bôcher Memorial Prize in 1964 for his work in mathematical analysis.

This result is possibly the most famous non-trivial example illustrating the incompleteness of a formal system.

Alexander GROTHENDIECK (University of Paris) - Built on work of Weil and Zariski and effected fundamental advances in algebraic geometry. He introduced the idea of K-theory (the Grothendieck groups and rings). Revolutionized homological algebra in his celebrated "Tohoku paper".

Alexander Grothendieck (Berlin, March 28,1928) was one of the most important mathematicians active in the 20th century. He was also one of its most extreme scientific personalities, with achievements over a short span of years that are still scarcely credible in their broad scope and sheer bulk, and an approach that antagonised even close followers. He made major contributions to algebraic geometry, homological algebra, and functional analysis. He was awarded the Fields Medal in 1966, and co-awarded the Crafoord Prize with Pierre Deligne in 1988. He declined the latter prize, on ethical grounds.

He is noted for his mastery of abstract approaches to mathematics, and his perfectionism in matters of formulation and presentation. Relatively little of his work after 1960 was published by the conventional route of the learned journal, circulating initially in duplicated volumes of seminar notes; his influence was to a considerable extent personal, on French mathematics and the Zariski school at Harvard University. He is the subject of many stories and some misleading rumours, concerning his work habits and politics, confrontations with other mathematicians and the French authorities, his withdrawal from mathematics at age 42, his retirement and his subsequent lengthy writings.

Stephen SMALE (University of California, Berkeley) - Worked in differential topology where he proved the generalized Poincaré conjecture in dimension n>=5: Every closed, n-dimensional manifold homotopy-equivalent to the n-dimensional sphere is homeomorphic to it. Introduced the method of handle-bodies to solve this and related problems.

Stephen Smale (born July 15,1930) is an American mathematician from Flint, Michigan, and winner of the Fields Medal in 1966. He made his reputation by a proof of the Poincare conjecture for all dimensions greater than 4; he later generalized the ideas in the proof to establish the h-cobordism theorem. Stephen Smale is also famous for the proof of sphere eversion (turning a sphere inside out without creating any crease).

After having made great strides in topology, he then turned to the study of dynamical systems, where he made significant advances as well as outlining a research program carried out by many others. The Smale horseshoe is an important example that jumpstarted significant research. Smale is also known for work in mathematical economics, as well as recent explorations of various theories of computation.

In 1998 he constructed a list of 18 problems in mathematics to be solved in the 21st century. This list was compiled in the spirit of Hilbert's famous list of problems produced in 1900. In fact, Smale's list includes some of the original Hilbert problems. Smale's problems include the Jacobian conjecture and the Riemann hypothesis, both of which are still unsolved.

Earlier in his career, he was involved in controversy over remarks he made regarding his work habits while proving the higher dimensional Poincare conjecture. This led to the withholding of his grant money from the NSF.

Smale has been politically active in various movements in the past, such as the Free Speech movement. At one time he was subpoenaed by the House Un-American Activities Committee.

Smale was also not a good student, earning B's and C's in many of his mathematics and physics courses while at the University of Michigan.

He is a triple-degree alumnus from the University of Michigan, where he earned his bachelor's degree in 1952, his master's degree in 1953, and his Ph.D. in 1957.

Smale is currently a professor at the Toyota Technical Institute at the University of Chicago.

1970

Alan BAKER (Cambridge University) - Generalized the Gelfond-Schneider theorem (the solution to Hilbert's seventh problem). From this work he generated transcendental numbers not previously identified.

Alan Baker (born on August 19, 1939) is an English mathematician. He was born in London. He is known for his work on effective methods in number theory, in particular those arising from transcendence theory. He was awarded the Fields Medal in 1970, at age 31. His academic career started as a student of Harold Davenport, at University College London and later at Cambridge. He is a fellow of Trinity College, Cambridge.

His interests are:

1. Number theory,
2. Transcendence,
3. Logarithmic forms,
4. Effective methods,
5. Diophantine geometry,
6. Diophantine analysis.

His students include John Coates, David Masser, Roger Heath-Brown, and Cameron Stewart
.

Heisuke HIRONAKA (Harvard University) - Generalized work of Zariski who had proved for dimension <=3 the theorem concerning the resolution of singularities on an algebraic variety. Hironaka proved the results in any dimension.

Heisuke Hironaka (広中 平祐 Hironaka Heisuke; April 9,1931–) is a Japanese mathematician. He received his Ph. D. from Harvard, under the directioni of Oscar Zariski. He won the Fields Medal in 1970.

He is celebrated for proving in 1964 that singularities of algebraic varieties admit resolutions in characteristic zero. This means that any projective variety can be replaced by a similar one (i.e. birationally equivalent) which has no singularities.

Hironaka was for many years a professor of mathematics at Harvard but currently lives in Japan, where he is greatly respected and influential. He has been active in raising funds for causes such as mathematical education.

Serge NOVIKOV (Belorusskii University) - Made important advances in topology, the most well-known being his proof of the topological invariance of the Pontrjagin classes of the differentiable manifold. His work included a study of the cohomology and homotopy of Thom spaces.

Sergei Petrovich Novikov (also Serguei) (Russian: Сергей Петрович Новиков) (born 20 March 1938) is a Russian mathematician, noted for work in both algebraic topology and soliton theory. He was born in Gorky, Russian SFSR (now Nizhny Novgorod, Russia).

Sergei grew up in a family of talented mathematicians. His father was Pyotr Sergeyevich Novikov, who gave the negative solution of the word problem for groups. His mother Ludmila and uncle Mstislav were also important mathematicians.

In 1955 Novikov entered the Moscow State University (graduated from it in 1960). Four years later he received the Moscow Mathematical Society Award for young mathematicians. In the same year he defended a dissertation for the Candidate of Science in Physics and Mathematics degree at the Moscow State University (it is equivalent to PhD). In 1965 he defended a dissertation for the Doctor of Science in Physics and Mathematics degree there. In 1966 he became the Corresponding member of the USSR Academy of Sciences.

His early work was in cobordism theory, in relative isolation. Among other advances he showed how the Adams spectral sequence, a powerful tool for proceeding from homology theory to the calculation of homotopy groups, could be adapted to the new (at that time) cohomology theory typified by cobordism and K-theory. This required the development of the idea of cohomology operations in the general setting, since the basis of the spectral sequence is the initial data of Ext functors taken with respect to a ring of such operations, generalising the Steenrod algebra. The resulting Adams-Novikov spectral sequence is now a basic tool in stable homotopy theory.

Novikov also carried out important research in geometric topology, and posed the Novikov conjecture. This work was recognised by the award in 1970 of the Fields Medal. From about 1971 he moved to work in the field of isospectral flows, with connections to the theory of theta functions.

Since 1971 Novikov has worked at the Landau Institute for Theoretical Physics of the USSR Academy of Sciences. In 1981 he was elected a Full Member of the USSR Academy of Sciences (Russian Academy of Sciences since 1991). In 1982 Novikov was also appointed the Head of the Chair in Higher Geometry and Topology at the Moscow State University.

As of 2004, Sergei is the Head of the Department of geometry and topology at the Steklov Mathematical Institute, he also teaches at the University of Maryland, College Park and is a Principal Researcher of the Landau Institute for Theoretical Physics in Moscow.

In 2005 Novikov was awarded the Wolf Prize for his contributions to algebraic topology, differential topology and to mathematical physics. He became one of just eight mathematicians who received both the Fields Medal and the Wolf Prize.

John Griggs THOMPSON (University of Chicago) - Proved jointly with W. Feit that all non-cyclic finite simple groups have even order. The extension of this work by Thompson determined the minimal simple finite groups, that is, the simple finite groups whose proper subgroups are solvable.

John Griggs Thompson (born 13 Oct 1932 in Kansas (USA) ) is a mathematician noted for his work in the field of finite groups. He received his B.A. from Yale University in 1955 and his doctorate from the University of Chicago in 1959 under the supervision of Saunders Mac Lane. In 1970 he moved to Cambridge, England, and later moved to the University of Florida. He is currently Rouse Ball Professor Emeritus of Pure Mathematics at Cambridge University and professor of mathematics at the University of Florida.

Thompson was a key figure in the progress toward the classification of finite simple groups. In 1963, he and Walter Feit proved that all nonabelian finite simple groups are of even order (the Odd Order Paper, filling a whole issue of the Pacific Journal of Mathematics). In the next few years he classified all the minimal finite simple groups: those that contain no other simple groups as subquotients. This work was later extended by many mathematicians to the classification of finite simple groups. Thompson received the Fields Medal in 1970.

He has also made major contributions to the inverse Galois problem. He found a criterion for a finite group to be a Galois group, that in particular implies that the monster simple group is a Galois group.

1974

Enrico BOMBIERI (University of Pisa) - Major contributions in the primes, in univalent functions and the local Bieberbach conjecture, in theory of functions of several complex variables, and in theory of partial differential equations and minimal surfaces - in particular, to the solution of Bernstein's problem in higher dimensions.

Enrico Bombieri (born November 26, 1940) is a Italian mathematician, born in Milan. He is now at the Institute for Advanced Study. He is known for work in number theory, algebraic geometry, and mathematical analysis. He was awarded a Fields Medal in 1974.

Bombieri's theorem is one of the major applications of the large sieve method. It improves Dirichlet's theorem on prime numbers in arithmetic progressions, by showing that by averaging over the modulus over a range, the mean error is much less than can be proved in a given case. This result can sometimes substitute for the still-unproved generalized Riemann hypothesis.

David Bryant MUMFORD (Harvard University) - Contributed to problems of the existence and structure of varieties of moduli, varieties whose points parametrize isomorphism classes of some type of geometric object. Also made several important contributions to the theory of algebraic surfaces.

David Bryant Mumford (born 11 June 1937) is an American mathematician known for distinguished work in algebraic geometry, and then for research into vision and pattern theory. He is currently a professor in the Division of Applied Mathematics at Brown University, having previously had a long academic career at Harvard University. He was born in Worth, in Sussex in England, of an English father and American mother.

At Harvard, Mumford became a student of Oscar Zariski, and his work in geometry always combined the traditional geometric insights with the latest algebraic techniques. He published on moduli spaces, with a theory summed up in his book Geometric Invariant Theory, on the equations defining an abelian variety, and on algebraic surfaces. His books Abelian Varieties (with C. P. Ramanujam) and Curves on an Algebraic Surface combined the old and new theories (to the disadvantage of the former, it has been claimed by Shreeram Abhyankar). His lecture notes on scheme theory circulated for years in unpublished form, at a time when they were the only accessible introduction. They are now available as The Red Book of Varieties and Schemes.

Other work that was less thoroughly written up were lectures on varieties defined by quadrics, and a study of Shimura's many papers from the 1960s.

Mumford’s research did much to revive the classical theory of theta functions, by showing that its algebraic content was large, and enough to support the main parts of the theory by reference to finite analogues of the Heisenberg group. He published some further books of lectures on the theory.

He also was one of the founders of the toroidal embedding theory; and sought to apply the theory to Gröbner basis techniques, through students who worked in algebraic computation.

He was awarded a Fields Medal in 1974. During the 1980s he left algebraic geometry, in order to study brain structure. He was a MacArthur Fellow from 1987 to 1992.

In 2002, he wrote a book with Caroline Series and David Wright on the visual geometry of limit sets: Indra's Pearls: The Vision of Felix Klein ISBN 0521352533.

His current area of work is pattern theory.

1978

Pierre René DELIGNE (Institut des Hautes Études Scientifiques) - Gave solution of the three Weil conjectures concerning generalizations of the Riemann hypothesis to finite fields. His work did much to unify algebraic geometry and algebraic number theory.

Pierre Deligne (born 3 October 1944) is a Belgian mathematician. He is known for fundamental work on the Weil conjectures, leading finally to a complete proof in 1973. He was born in Brussels.

After completing a doctorate, he worked with Alexander Grothendieck at the Institut des Hautes Études Scientifiques near Paris, initially on the generalisation within scheme theory of Zariski's main theorem. He worked closely with Jean-Pierre Serre, leading to important results on the l-adic representations attached to modular forms, and the conjectural functional equations of L-functions. He also collaborated with David Mumford on a new description of the moduli spaces for curves: this work has been much used in later developments arising from string theory.

From 1970 until 1984, when he moved to the Institute for Advanced Study in Princeton, Deligne was a permanent member of the IHÉS staff. During this time he did much important work, besides the proof of the Weil conjectures: in particular with George Lusztig on the use of étale cohomology to construct representations of algebraic groups, and with Rapoport on the moduli spaces from the 'fine' arithmetic point of view, with application to modular forms. He received a Fields Medal in 1978.

In terms of the completion of some of the underlying Grothendieck program of research, he defined absolute Hodge cycles, as a surrogate for the missing and still largely conjectural theory of motives. This idea allows one to get around the lack of knowledge of the Hodge conjecture, for some applications. He reworked the tannakian category theory in his paper for the Grothendieck Festschrift, employing Beck's theorem – the Tannakian category concept being the categorical expression of the linearity of the theory of motives as the ultimate Weil cohomology. All this is part of the yoga of weights, uniting Hodge theory and the l-adic Galois representations. The Shimura variety theory is related, by the idea that such varieties should parametrize not just good (arithmetically interesting) families of Hodge structures, but actual motives. This theory isn't yet a finished product – and more recent trends have used K-theory approaches.

Deligne has written a book with G. D. Mostow on monodromy. He was awarded the Crafoord Prize in 1988.

Charles Louis FEFFERMAN (Princeton University) - Contributed several innovations that revised the study of multidimensional complex analysis by finding correct generalizations of classical (low-dimensional) results.

Charles Louis Fefferman (born April 18,1949) is a renowned mathematician at Princeton University. He won the Fields medal in 1978 for work in mathematical analysis. Another notable honour attached to his name is that of being the youngest full professor at a university in the United States. A child prodigy, Fefferman had entered college by twelve and had written his first scientific paper by the age of 15 in German. After receiving his bachelor's degrees in physics and mathematics at the age of 17 from the University of Maryland and a PhD in mathematics at 20 from Princeton University, Fefferman received full professorship at the University of Chicago at the age of 22. At 24, he returned to Princeton to assume a full professorship there - a position he still holds.

His early work included a study of the asymptotics of the Bergmann kernel off the boundaries of pseudoconvex domains in .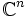

Gregori Aleksandrovitch MARGULIS (Moscow University) - Provided innovative analysis of the structure of Lie groups. His work belongs to combinatorics, differential geometry, ergodic theory, dynamical systems, and Lie groups.

Gregori Aleksandrovich Margulis (first name often given as Gregory,Grigori or Grigory) (born February 24, 1946) is a mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in 2005 (joining six mathematicians, up to 2004, who had received both prizes).

He was born into a Jewish family in Moscow, USSR. He studied at Moscow State University, starting research in ergodic theory. Early work with David Kazhdan produced the Kazhdan-Margulis theorem, a basic result on discrete groups. His superrigidity theorem from 1975 clarified a whole area of classical conjectures about the characterisation of arithmetic groups amongst lattices in Lie groups.

He was awarded the Fields Medal in 1978, but was not permitted to travel to Helsinki to accept in person. His position improved, and 1979 he visited Bonn, and was later able to travel freely, though he still worked in a technical institute rather than a mathematics department. In 1991 he took a professorial position at Yale University.

In 1986, Margulis completed the proof of the Oppenheim conjecture on quadratic forms and diophantine approximation. This was a question that had been open for half a century, on which considerable progress had been made by the Hardy-Littlewood circle method; but to reduce the number of variables to the point of getting the best-possible results, the more structural methods from group theory proved decisive. He has formulated a further program of research in the same direction, that includes the Littlewood conjecture. This has been widely influential.

In 2005, Margulis received the Wolf Prize for his contributions to lattice theory, and applications to ergodic theory, representation theory, number theory, combinatorics, and measure theory.

Daniel G. QUILLEN (Massachusetts Institute of Technology) - The prime architect of the higher algebraic K-theory, a new tool that successfully employed geometric and topological methods and ideas to formulate and solve major problems in algebra, particularly ring theory and module theory.

Quillen was born in Orange, New Jersey. He entered Harvard University, where he earned both his BA (1961) and his PhD (1964), the latter of which was completed under the supervision of Raoul Bott with a thesis in partial differential equations.

Quillen obtained a position at the Massachusetts Institute of Technology after completing his doctorate. However, he also spent a number of years at several other universities. This experience would prove to be important in influencing the direction of his research. He visited France twice: first as a Sloan Fellow in Paris, during the academic year 1968–69, where he was greatly influenced by Grothendieck, and then, during 1973–74, as a Guggenheim Fellow. In 1969–70, he was a visiting member of the Institute for Advanced Study at Princeton, where he came under the influence of Atiyah.

Before his ground-breaking work in defining higher algebraic K-theory, Quillen worked on the Adams conjecture, formulated by Frank Adams in homotopy theory. His proof of the conjecture used techniques from the modular representation theory of groups, which he later applied to work on cohomology of groups and algebraic K-theory.

In 1978, Quillen received a Fields Medal at the International Congress of Mathematicians held in Helsinki. He received the award for successfully formulating higher algebraic K-theory in 1972, a problem that had baffled mathematicians since algebraic K-theory was first formulated. This new tool, formulated in terms of homotopy theory, proved to be successful in formulating and solving major problems in algebra, particularly in ring theory and module theory. Amongst his collaborating mathematicians is his former pHd student Mathai Varghese

In related work, he also supplied a proof of Serre's conjecture about the trivality of algebraic vector bundles on affine space.

1982

Alain CONNES (Institut des Hautes Études Scientifiques) - Contributed to the theory of operator algebras, particularly the general classification and structure theorem of factors of type III, classification of automorphisms of the hyperfinite factor, classification of injective factors, and applications of the theory of C*-algebras to foliations and differential geometry in general.

Alain Connes (born April 1,1947) is a French mathematician, currently Professor at the College de France (Paris, France), IHES (Bures-sur-Yvette, France) and Vanderbilt University (Nashville,Tennessee). He is a specialist of Von Neumann algebras and succeeded in completing the classification of factors of these objects. Although his work in physics was not very convincing he tried to connect the planckian scales with what he called a "2-brane" Universe, model which was largely rejected by string theorists so far.

The remarkable links between this subject, the tools he and others devised to tackle the problem and other subjects in theoretical physics, particle physics, and differential geometry, made him emphasize Noncommutative geometry (which is also the title of his major book to date).

He was awarded the Fields Medal in 1982, the Crafoord Prize in 2001 and the gold medal of the CNRS in 2004.

William P. THURSTON (Princeton University) - Revolutionized study of topology in 2 and 3 dimensions, showing interplay between analysis, topology, and geometry. Contributed idea that a very large class of closed 3-manifolds carry a hyperbolic structure.

William Paul Thurston (born October 30, 1946) is an American mathematician. He was born in Washington, D.C and received his bachelors degree from New College (now New College of Florida) in 1967 followed by a doctorate from the University of California, Berkeley, in 1972. His Ph.D. advisor was Morris W. Hirsch.

He is currently a professor at Cornell University. Previously he was at UC Davis, from 1996 to 2003. In the interim, he has taught both at Berkeley and Princeton. His Ph.D. students include David Gabai, Jeff Weeks, Craig Hodgson, Steven Kerckhoff, Yair Minsky, Robert Meyerhoff, Oded Schramm, William Goldman, and Richard Schwartz.

In 1982, he was awarded the Fields medal for the depth and originality of his contributions to mathematics. His fresh insights have linked many apparently disparate fields to 3-manifolds. Thurston's geometrization conjecture (and all it entails) revolutionized 3-manifold theory, reviving hyperbolic geometry. His early work was mainly in foliation theory, where he proved, amongst other things, that any n-manifold with Euler characteristic zero has a codimension one foliation.

Thurston has turned his attention in recent years to mathematical education and bringing mathematics to the general public. He has served as mathematics editor for Quantum magazine, a youth science magazine, and as head of the University of Minnesota Geometry Center. As director of Mathematical Sciences Research Institute from 1992 to 1997, he initiated a number of programs designed to increase awareness of mathematics among the public.

Shing-Tung YAU (Institute for Advanced Study) - Made contributions in differential equations, also to the Calabi conjecture in algebraic geometry, to the positive mass conjecture of general relativity theory, and to real and complex Monge-Ampère equations.

Shing-Tung Yau (丘成桐; Pinyin: Qīu Chéngtóng; born April 4, 1949) is a prominent mathematician working in differential geometry, and involved in the theory of Calabi-Yau manifolds.

He was born in Shantou, Guangdong Province, China with an ancestry in Jiaoling (also in Guangdong) in a family of eight children. His father, a professor teaching philosophy, died when he was 14. Yau moved to Hong Kong with his family where, after graduating from Pui Ching Middle School, he studied mathematics at the Chinese University of Hong Kong from 1966 to 1969. He undertook graduate studies at the University of California, Berkeley, where his advisor was Shiing-Shen Chern. After receiving his Ph.D. in 1971, he spent a post-doctoral year at the Institute for Advanced Study. He then spent two years as an assistant professor at Stony Brook University.

In 1974 he was appointed a professor at Stanford University. He returned to the Institute for Advanced Study as a professor in 1979. In that year, together with his former doctoral student Richard Schoen, he proved the positive energy theorem in general relativity. From 1984 to 1987 he was a professor at UC San Diego. In 1987 he moved to Harvard University, where he remains.

Yau has received a number of prominent awards. These include the Fields Medal in 1983 "for his contributions to partial differential equations, to the Calabi conjecture in algebraic geometry, to the positive mass conjecture of general relativity theory, and to real and complex Monge-Ampère equations", a MacArthur Fellowship in 1984, the Crafoord Prize in 1994, and the (U.S.) National Medal of Science in 1997.

His name is romanized according to its pronunciation in Cantonese Chinese.

1986

Simon K. DONALDSON (Oxford University) - Received medal primarily for his work on topology of four-manifolds, especially for showing that there is a differential structure on euclidian four-space which is different from the usual structure.

Simon Kirwan Donaldson, born in Cambridge in 1957, is a mathematician famous for his work on the topology of smooth (differentiable) four-dimensional manifolds.

Donaldson gained a BA in mathematics from Pembroke College, Cambridge in 1979, and in 1980 began postgraduate work at Worcester College, Oxford, first under Nigel Hitchin and later under Atiyah's supervision. Still a graduate student, Donaldson soon proved in 1982 a result that would establish his fame. He published the result in a paper Self-dual connections and the topology of smooth 4-manifolds which appeared in 1983. In the words of Atiyah, the paper "stunned the mathematical world".

Whereas Michael Freedman classified topological four-manifolds, Donaldson's work focused on four-manifolds admitting a differentiable structure, using instantons, a particular gauge theory which has its origin in quantum field theory. One of Donaldson's first results gave severe restrictions on the intersection form of a smooth four-manifold. As a consequence, a large class of the topological four-manifolds do not admit any smooth structure at all. Donaldson also derived polynomial invariants from gauge theory. These were new topological invariants sensitive to the underlying smooth structure of the four-manifold. They made it possible to deduce the existence of "exotic" smooth structures - certain topological four-manifolds could carry an infinite family of different smooth structures.

After gaining his doctorate from Oxford University in 1983, Donaldson was appointed a Junior Research Fellow at All Souls College, Oxford, he spent the academic year 1983–84 at the Institute for Advanced Study at Princeton, and returned to Oxford as Wallis Professor of Mathematics in 1985. In 1999, he moved to Imperial College London.

Donaldson received the Junior Whitehead Prize from the London Mathematical Society in 1985 and in the following year he was elected a Fellow of the Royal Society and, also in 1986, he received a Fields Medal. Ironically he was turned down for fellowship of the Institute of Mathematics and its Applications on the grounds that he applied too soon after his doctorate! He was awarded the 1994 Crafoord Prize.

Gerd FALTINGS (Princeton University) - Using methods of arithmetic algebraic geometry, he received the medal primarily for his proof of the Mordell Conjecture.

Michael H. FREEDMAN (University of California, San Diego) - Developed new methods for topological analysis of four-manifolds. One of his results is a proof of the four-dimensional Poincaré Conjecture.

Michael Hartley Freedman (born 21 April 1951 in Los Angeles, California, USA) is a mathematician at Microsoft Research. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture, one of the most famous problems of the 20th century.

The Poincaré conjecture asserts that a simply connected closed 3-dimensional manifold is a 3-dimensional sphere. The higher dimensional Poincaré conjecture claims that any closed n-manifold which is homotopy equivalent to the n-sphere must be the n-sphere. When n = 3 this is equivalent to the Poincaré conjecture. Smale proved the higher dimensional Poincaré conjecture in 1961 for n at least 5. Freedman proved the conjecture for n = 4 in 1982. Grigori Perelman is thought to have recently proved the remaining case of n=3.

Freedman was awarded a doctorate by Princeton University in 1973 for his doctoral dissertation entitled Codimension-Two Surgery. After graduating Freedman was appointed a lecturer in the Department of Mathematics at the University of California, Berkeley. He held this post from 1973 until 1975 when he became a member of the Institute for Advanced Study at Princeton. In 1976 he was appointed as assistant professor in the Department of Mathematics at the University of California, San Diego (UCSD). He spent the year 1980/81 at the Institute for Advanced Study at Princeton returning to UCSD where he was promoted to professor on 1982. He was appointed the Charles Lee Powell chair of mathematics at UCSD in 1985.

He has received numerous other awards and honors including Sloan and Guggenheim Fellowships, a MacArthur Fellowship and the National Medal of Science. He is an elected member of the National Academy of Sciences, the American Academy of Arts and Sciences, and the New York Academy of Sciences.

He currently works at University of California, Santa Barbara where his team is involved in the development of the Quantum Computer. He also enjoys rock climbing and spending time with his wife, Sam, and three sons: Hartley, Whitney, and Jake.

1990

Vladimir DRINFELD (Phys. Inst. Kharkov) - Made significant contributions to Langland's program and quantum groups.

Vladimir Gershonovich Drinfel'd (Владимир Гершонович Дринфельд) is a mathematician born February 14, 1954 in Ukraine.

He won a gold medal in International Mathematics Olympiad in 1969, representing the Soviet Union, at the age of 15, and entered university after this.

In 1986, he gave a seminal address to the International Congress of Mathematicians at Berkeley, where he coined the term "Quantum Group" in reference to Hopf algebras which were deformations of simple Lie algebras, and connected them to the study of the Yang-Baxter equation, a necessary condition for the solvability of statistical mechanical models. He also generalized Hopf algebras to quasi-Hopf algebras, and introduced the study of Drinfeld twists, which can be used to factorize the R-matix corresponding to the solution of the Yang-Baxter equation associated with a quasitriangular Hopf algebra.

He was awarded a Fields Medal in 1990, and is currently the Harry Pratt Judson Distinguished Service Professor at the University of Chicago.

He is known for work in number theory and other fields; in particular for his proof of the substantive part of the Langlands program for GL₂ of a function field of an algebraic curve over a finite field, this being the first major non-abelian case over a global field that was known.

Vaughan F.R. JONES (University of California, Berkeley) - Proved the Index Theorem and discovered a relationship between Von Neumann algebras and geometric topology.

Vaughan Frederick Randal Jones (born 31 December 1952) is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize. Jones is a professor at the University of California, Berkeley and a Distinguished Alumni Professor at the University of Auckland.

He was born in Gisborne, New Zealand and brought up in Cambridge, New Zealand. His undergraduate studies were at the University of Auckland, after which he travelled widely abroad.

His work on knot polynomials, with the discovery of what is now called the Jones polynomial, was from an unexpected direction with origins in functional analysis, as conceived by Alain Connes. It led to the solution of a number of the classical problems of knot theory, and to increased interest in low-dimensional topology.

Shigefumi MORI (University of Kyoto) - Work in algebraic geometry developed the Mori Program in connection with the classification problems of algebraic varieties of dimension three.

Shigefumi Mori (森 重文 Mori Shigefumi, born February 23, 1951) is a Japanese mathematician, known for his work in algebraic geometry, particularly in relation to the classification of three-folds.

He generalized the classical approach to the classification of algebraic surfaces to the classification of algebraic three-folds. The classical approach used the concept of minimal models of algebraic surfaces. He found that the concept of minimal models can be applied to three-folds as well if we allow some singularities on them.

The extension of Mori's results to dimensions higher than three is called the Mori program and as of 2005, is an extremely active area of algebraic geometry.

He was awarded the Fields Medal in 1990 at the International Congress of Mathematicians.

Edward WITTEN (Institute for Advanced Study, Princeton) - Completed an amazing proof of the classic Morse inequalities and gave a proof of positivity of energy in Einstein's theory of Gravitation.

Witten was born in Baltimore, Maryland, the son of Lorraine Wollach Witten and Louis Witten, a physicist specializing in gravitation and general relativity. He received his bachelor's degree from Brandeis University, worked briefly for George McGovern's presidential campaign, and then returned to academia, receiving a Ph.D. from Princeton University in 1976. Afterwards, he worked at Harvard University as a Junior Fellow and at Princeton as a professor. He is currently the Charles Simonyi Professor of Mathematical Physics at the Institute for Advanced Study.

Witten's work combines deep physical insight with a remarkable command of modern mathematics. He has been active primarily in quantum field theory and string theory, and in related areas of topology and geometry. Among his many contributions are his proof of the positive energy theorem in general relativity, his work relating supersymmetry and Morse theory, his introduction of topological quantum field theory and his related work on mirror symmetry and supersymmetric gauge theories, and his conjecture of the existence of M-theory.

Witten is widely admired among his fellows. Among those who praise him is Sir Michael Atiyah, who said,

"Although he is definitely a physicist, his command of mathematics is rivaled by few mathematicians... Time and time again he has surprised the mathematical community by his brilliant application of physical insight leading to new and deep mathematical theorems... he has made a profound impact on contemporary mathematics. In his hands physics is once again providing a rich source of inspiration and insight in mathematics."

Likewise, in his bestseller The Elegant Universe, Columbia University physicist Brian Greene writes that Witten is "widely regarded as Einstein's successor in the role of the world's greatest living physicist."

Witten has been honored with numerous awards, including a MacArthur Grant, a Fields Medal, and the National Medal of Science (2004). He also appeared in the List of TIME Magazine's 100 most influential people of 2004. Witten has the highest H Index of any living physicist

1994

Jean BOURGAIN (Institute for Advanced Study, Princeton) - work in a variety of different mathematical areas such as Banach spaces, convexity in high dimensions, harmonic analysis, ergodic theory and nonlinear partial differential equations.

Pierre-Louis LIONS (Université de Paris-Dauphine) - awarded the medal for his work on the theory of nonlinear partial differential equations.

He studies the theory of nonlinear partial differential equations, and received the Fields Medal for his work in 1994. Lions also worked on the Boltzmann equation. He was the first to give a complete solution to the Boltzmann equation with a proof. Other awards Lions received include the IBM Prize in 1987 and the Philip Morris Prize in 1991.

Jean-Christophe YOCCOZ (Université de Paris-Sud) - achieved many important results in dynamical systems.

French mathematician who was awarded the Fields Medal in 1994 for his work in dynamical systems

Yoccoz was educated at the École Normale Supérieure, Paris, and the École Polytechnique, Palaiseau (Ph.D., 1985). He then became a professor at the University of Paris at Orsay.

Yoccoz was awarded the Fields Medal at the International Congress of Mathematicians in Zürich.

Efim ZELMANOV (University of Wisconsin) - solved the restricted Burnside problem.

Efim Isaakovich Zelmanov (Ефим Исаакович Зельманов: born September 7, 1955) is a mathematician, known for his work on combinatorial problems in nonassociative algebra and group theory, including his solution of the restricted Burnside problem. He was awarded a Fields Medal in 1994.

He was born into a Jewish family in Khabarovsk,Soviet Union (Russia). He took a doctoral degree at Novosibirsk University, and a higher degree at Leningrad State University in 1985. He had a position in Novosibirsk until 1987, when he left the Soviet Union.

From 1990 he was professor at the University of Wisconsin-Madison; he was at the University of Chicago in 1994/5, then at Yale University.

As of 2002, he is professor at the University of California, San Diego.

His early work was on Jordan algebras in the case of infinite dimensions. He was able to show that Glennie's identity in a certain sense generates all identities that hold. He then showed that the Engel identity for Lie algebras implies nilpotence, in the case of infinite dimensions.

1998

Richard E. BORCHERDS (Cambridge University) - Awarded for work in Kac-Moody algebras and automorphic forms.

British mathematician who won the Fields Medal in 1998 for his work in algebra.

Borcherds studied undergraduate mathematics at the University of Cambridge and went on to finish his doctorate there in 1983. Afterward he held teaching and research positions at Cambridge and at the University of California at Berkeley.

W. Timothy GOWERS (Cambridge University) - Produced important results in Banach space theory and combinatorics.

Maxim KONTSEVIC (Institut des Hautes Études Scientifiques) - Work in mathematical physics, algebraic geometry and topology opening up new avenues in research.

Maxim Kontsevich (Russian: Максим Концевич) (born August 25, 1964) is a Russian mathematician. He graduated from the Moscow State University. In 1992 he received his Ph.D. at the University of Bonn, Germany with Don Bernard Zagier as his advisor. Currently he is a professor at the Institut des Hautes Études Scientifiques (IHÉS) in Bures-sur-Yvette, France and visiting professor at the Rutgers University in New Brunswick, New Jersey, USA. He has worked on geometrical aspects of knot theory and string theory. In 1998 at the 23rd International Congress of Mathematicians in Berlin, Germany he received the Fields Medal together with Richard Ewen Borcherds, William Timothy Gowers and Curtis T. McMullen. See also: Kontsevich integral

Curtis T. McMULLEN (Harvard University) - For his work in complex dynamics and hyperbolic geometry.

Curtis T McMullen (born 21 May 1958) is Professor of Mathematics at Harvard University. He won the Fields Medal in 1998 for his work, particularly in complex dynamics. He received his bachelor's degree in 1980 from Williams College and his Ph.D. in 1985 from Harvard University, supervised by Dennis Sullivan.

Research Interests :

McMullen's major work involved finding the relationship between the geometry of three-dimensional objects and the universal structure that occurs in the transition from regular to chaotic physical behavior.

His current research consist in using the deep link between chaos and rigidity to provide a geometric understanding of universal constants in dynamics.

2002

Vladimir VOEVODSKY (Institute for Advanced Study, Princeton) - was honored for making major advances in the "Langlands Program," based on a visionary set of conjectures by Robert Langlands that sketch out deep connections between number theory, analysis, and group representation theory. Lafforgue proved the global Langlands correspondence for function fields, building on the work of Vladimir Drinfeld (also a Fields medalist, in 1990).

Vladimir Voevodsky (Russian:Владимир Воеводский) (born June 4,1966) is a Russian mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.

Voevodsky received his Ph. D. in mathematics from Harvard University in 1992. Currently he is a full professor at the Institute for Advanced Study in Princeton,New Jersey.

Voevodsky's work is in the field of algebraic geometry. However, that field has always benefited from techniques introduced from algebraic topology. Voevodsky contributed to this by introducing a homotopy theory for algebraic varieties. He also formulated what is now believed to be the 'correct' form of motivic cohomology, and used this new tool to prove Milnor's conjecture relating the Milnor K-theory of a field to its étale cohomology. For the above, he received the Fields Medal, together with Laurent Lafforgue, at the 24th International Congress of Mathematicians held in Beijing,China.

He is coauthor (with Andrei Suslin and Eric M. Friedlander) of Cycles, Transfers and Motivic Homology Theories (Princeton University Press, 2000), which develops the theory of motivic cohomology in some detail.

Laurent LAFFORGUE (Institut des Hautes Études Scientifiques) - was honored for developing a new cohomology theory for algebraic varieties.

From Wikipedia, the free encyclopedia.

Laurent Lafforgue (born November 6, 1966) is a French mathematician.

Born in Antony, France. He entered the École Normale Supérieure in 1986. In 1994 he received his Ph.D. in the Arithmetic and Algebraic Geometry team at the Université de Paris-Sud. Currently he is a research director of CNRS, detached as permanent professor of mathematics at the Institut des Hautes Études Scientifiques (I.H.E.S) in Bures-sur-Yvette, France.

In 2002 at the 24th International Congress of Mathematicians in Beijing,China he received the Fields Medal together with Vladimir Voevodsky. Lafforgue made outstanding contributions to Langlands program in the fields of number theory and analysis.

The crucial contribution by Lafforgue to solve this question is the construction of compactifications of certain varieties of modules. The proof, which is monumental, is the result of more than six years of concentrated efforts.

2018??

John WUNDERLE (University of Liverpool) for exceptional work in proving the Birch and Swinnerton Dyer conjecture.